Backpropagation
HS 03/20/2018
一個Neural Network裡可能有上百萬的參數,在使用Gradient Descent作訓練時就會產生上百萬維的矩陣,如下圖一所示:

圖一
而我們可利用Backpropagation來讓訓練Neural Network變得更有效率。
而Backpropagation就是一種計算Gradient Descent會更有效率的演算法。
Backpropagation主要的數學是Chain rule,如下圖二所示:

圖二
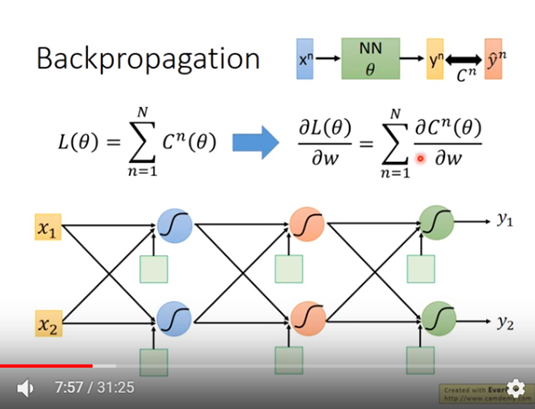
先看下圖三的一個Neural Network,輸入n筆input data: x,
會得到n筆output data: y,
而C是輸出output data與label data的距離。
定義Loss function為每筆data 的C值總合。
計算Loss function對其中一變數w偏微分時即是C值總合對變數w偏微分。
圖三
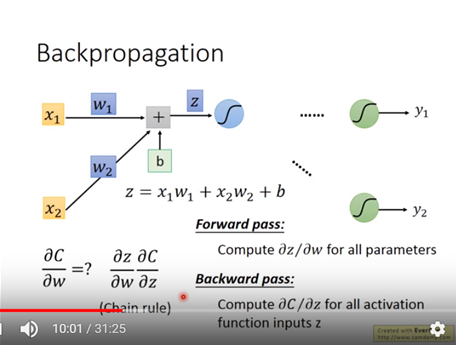
以圖四中Cost 對w作偏微分為範例(Cost對b作偏微分依些類推),其等於z對w作偏微分乘上Cost對z偏微分。其中z對w作偏微分稱作forward pass,Cost對z偏微分稱作backward pass。z 為activation function 的input。
圖四
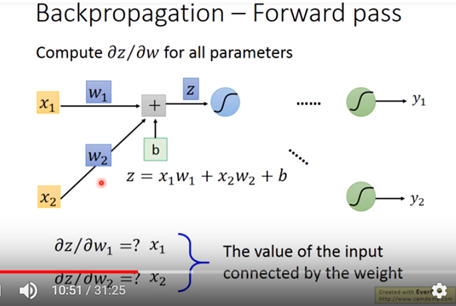
先看forward pass: z對w作偏微分 如下圖五 z對w作偏微分即為input x
圖五
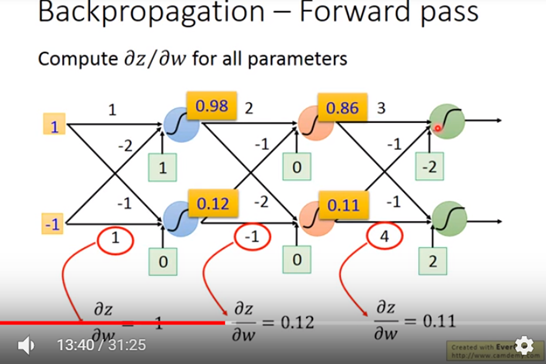
圖六所示 forward pass範例程序下的值。
圖六
再看Backward pass,Cost對z作偏微分可等於a對z作偏微分再乘上Cost對a作偏微分,a 為 neural的output。
其中a對z作偏微分為圖八sigmoid function 對z作偏微分。至於Cost function 對a作偏微分需用chain rule展開如圖七。z’對a的偏微分與z”對a的偏微分別為W3與W4,至於C對z’與C對z”偏微分值先假設已知,這些值可從最後一層的out 反推回來,目前就先假設已知,下面接續解釋。
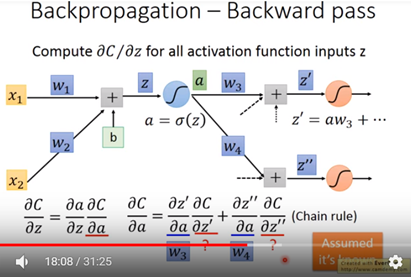
圖七
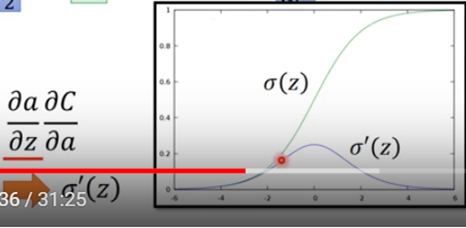
圖八
圖九所示整個backward pass公式,該公式其實可以看成圖九的一個反向的neural network如圖十所示。
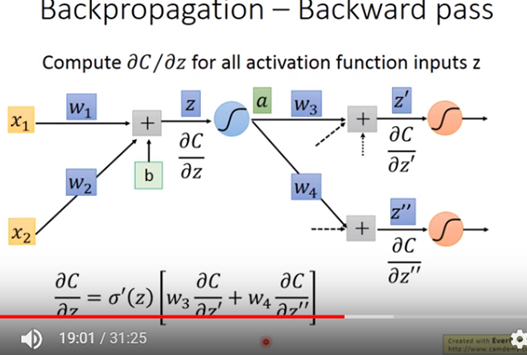
圖九
可看成一個新的neural network,但其是將兩個input各別乘上weighting後再乘上sigmoid對z的偏微份值後變成output。其中sigmoid對z的偏微份在forward pass時就計算出來了,故其是為一個常數。
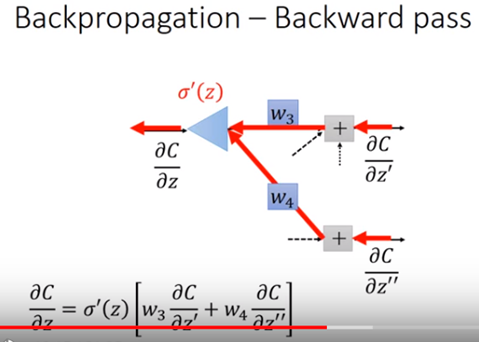
圖十
接下來假設回到C對z’與C對z”偏微分值是已知的問題,先討論case1是當C對z’與C對z”該層的neural已經是最後一層,如圖十一。其output分別是y1與y2。其C對z’可寫成y1對z’的偏微乘上C對y1的偏微分, 又y1對z’的偏微分即是activation對z’的微份值,而C對y1的偏微分值取決於你Cost function定義的方式,其也是已值,因此C對z’即能求得。同理,C對z”的微份值可能求得。如此backward pass就能完成。
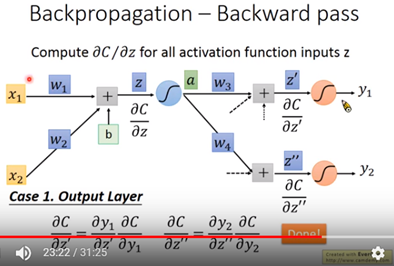
圖十一
接下來討論case2如圖十二,當C對z’與C對z”該層的neural還不是最後一層,此時需要再往下一層反推上來,即利用如上述的反向公式反推回來,如果下層還不是最後一層就一直往下層找到最後一層反推上來。
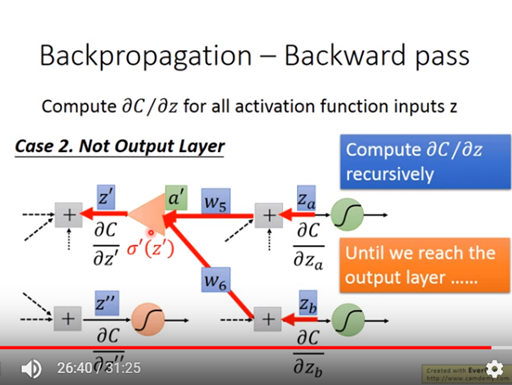
圖十二
最後給一個範例如圖十三,其告訴我們當我們想求得下圖十三裡C對w的偏微分時,其可看成如圖十四的backward pass的運作。先求到C對z5偏微分與C對z6偏微分再乘上weighting後,再各別乘上sigmoid對z3或z4的偏微份後,即往上一層推進。依此類推反推到最上層。
結論如圖十五,Cost C對w的的偏微分即拆成forward pass的結果乘上backward pass的結果。
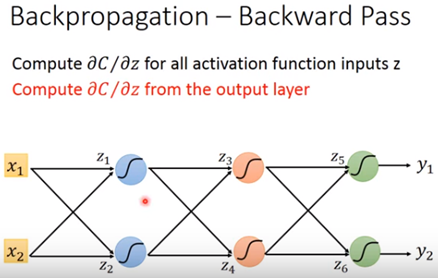
圖十三
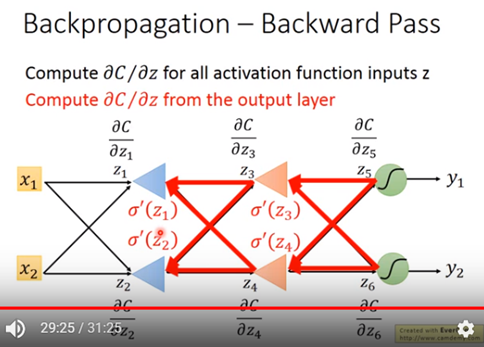
圖十四
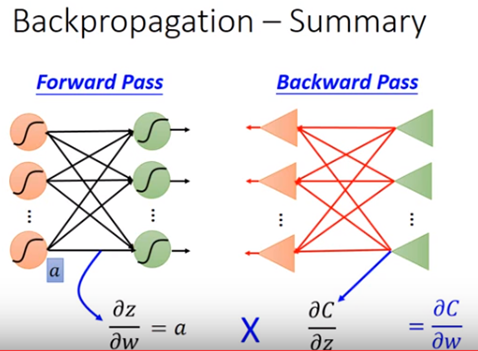
圖十五