Recurrent Neural Network (Professor 李宏毅 #21-1)

Tsung-Yung 3/20/2018

舉個例子，如果我們要建一個基於語音辨識的售票系統(ticket booking system)，它可以輸入一段語音，它可以從裡面挑出抵達日期(time of arrival)跟目的地(Destination)。

圖一 ticket booking system

如圖一所示，輸入一段文字 "I would like to arrive Taipei on November $2^{nd}$."，它能自動擷取目的地是Taipei，抵達日期是November $2^{nd}$。這樣的技術又稱作Slot Filling。

那我們要怎麼實作這個系統呢？我們可以使用簡單的Feedforward Network如圖二所示：
圖二 Feedforward Neural Network

把一個一個單字變成word vector輸入網路，在輸出有 $y_1$ 代表該單字是Destination的機率， $y_2$是抵達時間的機率。常見的word vector產生的方式有1-of-N encoding，但是詞語庫的字彙量一定遠遠小於現實世界的字彙量。為了更好表達這樣的情況，我們在原本N維再增加一維代表沒有在辭彙庫出現的字，另外還有一種方式叫word hashing，就是把一個英文字拆成字母的組合，以3維word hashing，總共會有26x26x26種組合，以單字apple為例，可以拆成a-p-p, p-p-l, p-l-e，代表這三個組合的維度會加1，其餘為0，這樣編碼的好處是可以用有限的維度表現所有的字彙組合。

用Feedforward網路的缺點是，以兩個句子為例 "I would like to arrive Taipei on November $2^{nd}$.", "I would like to leave Taipei on November $2^{nd}$." 在第二個句子裡面，Taipei並不是目的地，而是出發地。對於Feedforward網路而言，因為它是單個單字判斷，所以只要輸入相同，輸出的值就一定相同。解決的方式是讓神經網路擁有記憶力，才有辦法解決。

Recurrent Network就是讓網路具備記憶的一種方式。我們以ticket booking system為例，如圖三所示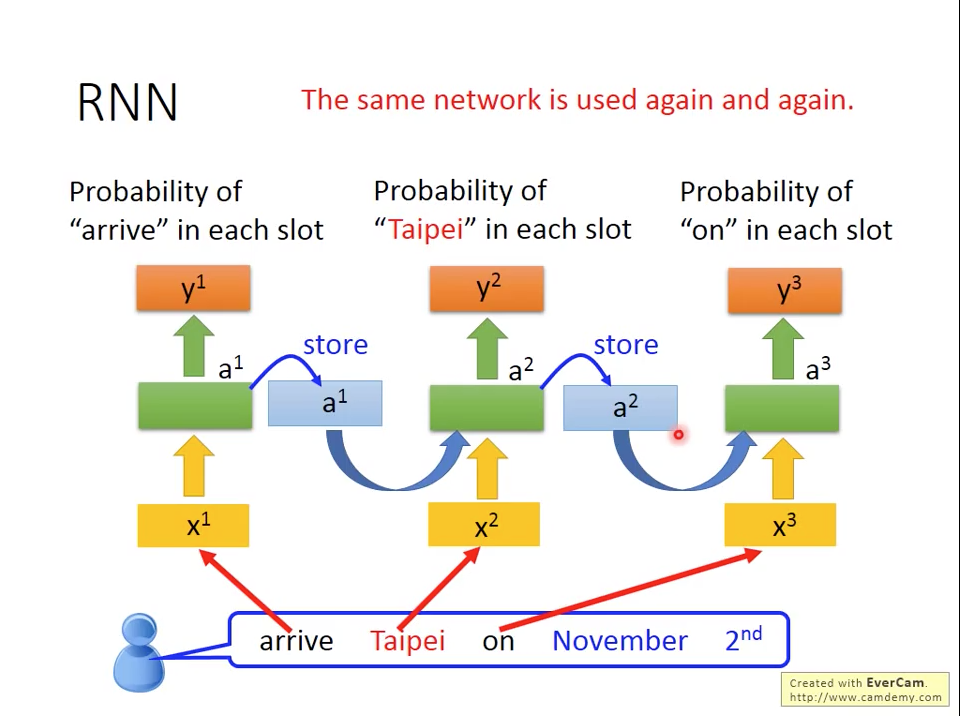： 圖三 ticket booking system using RNN 我們在不同的時間把單字依序輸入網路，輸出還是跟Feedforward network一樣是每個單字對目的地跟抵達日期的機率，不同的地方是 RNN會把隱藏層(hidden state)儲存起來，跟下個時間點單字同時輸入網路。圖三裡面畫法不是代表有三個獨立的網路，而是同一個RNN在不同時間點被重複使用。因為RNN有記憶功能，所以如圖四所示，對於我們之前舉的例子而言，雖然都是輸入"Taipei"，但是因為網路還有之前輸入是"leave"還是"arrive"，所以對於Probability of "Taipei"會不同。

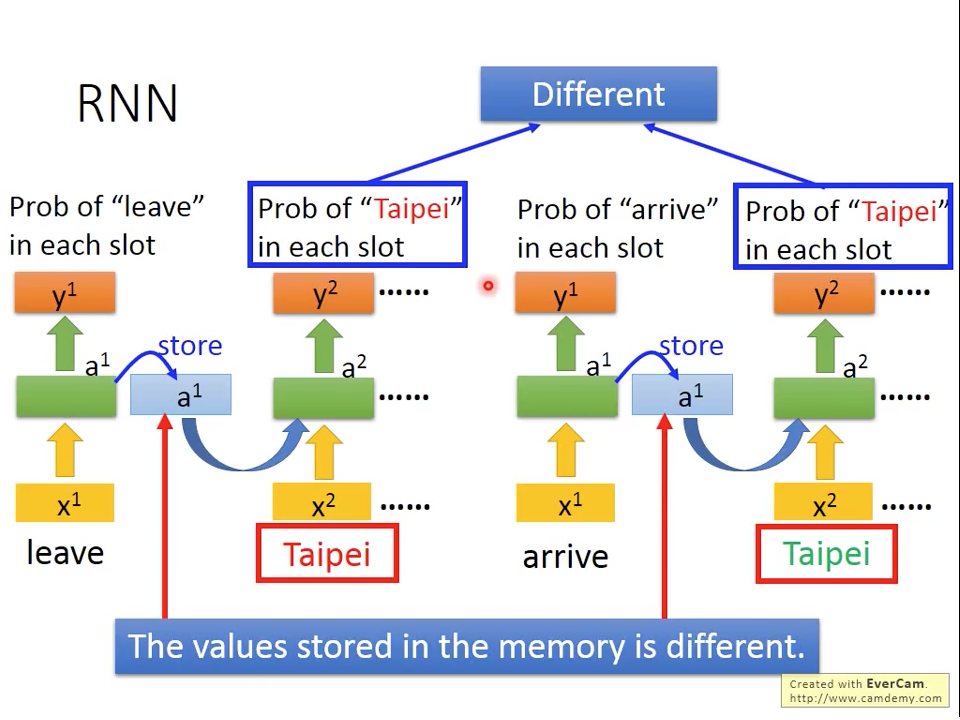圖四 How RNN solve Ticket Slot Problem

在RNN，我們常見的網路又稱作Elman Network(圖五)，另外還有另外一種Jordan Network，兩者的差異是Jordan Network儲存的不是隱藏層的資料，而是輸出層。根據李宏毅的survey，聽說Jordan network的performance會比Elman Network好一些，原因是Jordan Network直接是從輸出結果來直接影響網路，而不是Elman Network是比較間接。

Q by TY: 如果Jordan Network performance比較好，為什麼現在決大部分的RNN都是用Elman Network?

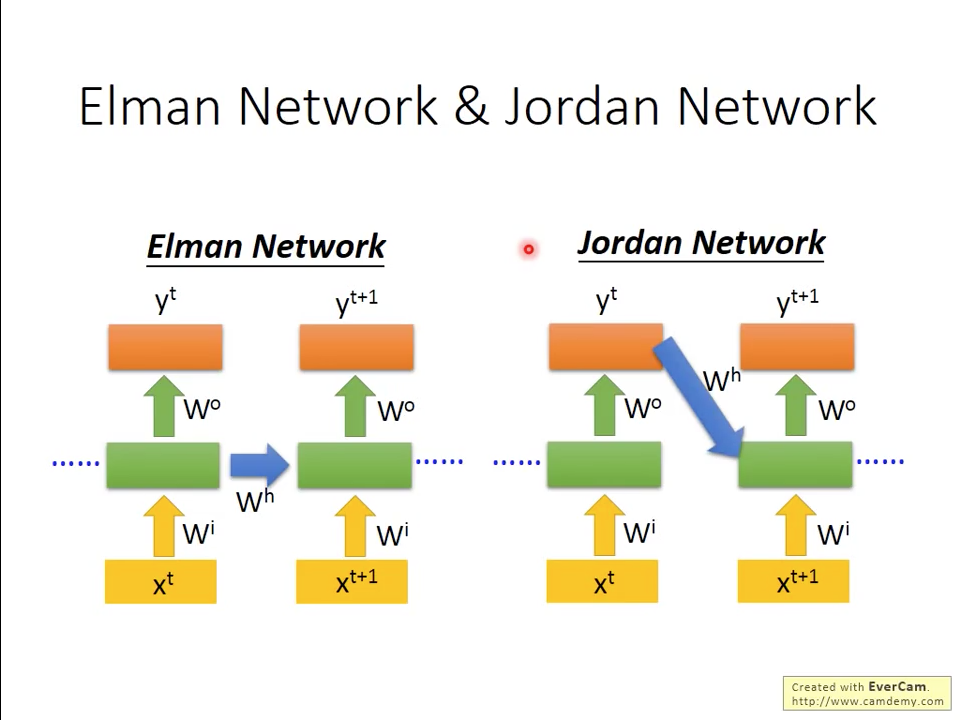圖五 Elman Network vs Jordan Network

除了單個時間由前到後的RNN之外，我們還可以把兩個RNN如圖六所示並聯起來，一個是正常時間方向，一個是反著時間方向，用順跟逆時間的資訊來預測每個時間點的輸出，這樣的網路叫做Bidirectional RNN，這樣架構的好處，可以讓每個時間的預測是參照全文的內容，而不是原本RNN，只看原本輸入之前的時間點。 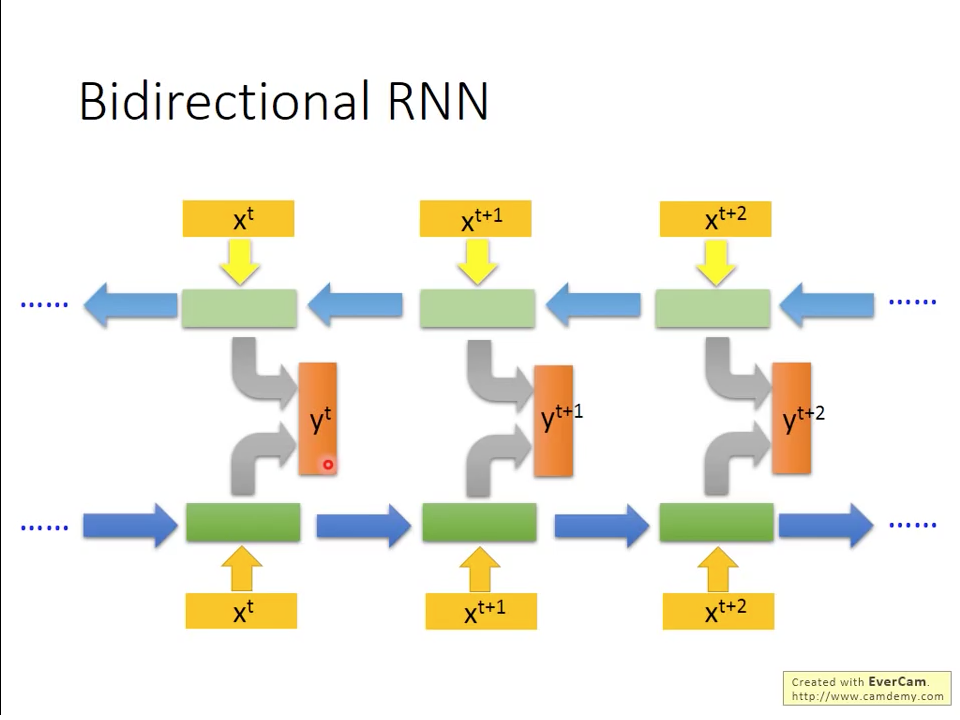圖六 Bi-directional RNN

LSTM

因為記憶結構限制，讓RNN能夠記憶只有前後幾個時間點的資訊，為了克服這個問題，又發展出長短期記憶元(long short-term memory)來捕捉比較長時間的訊號關係。LSTM在原本的Memory cell加入門(gate)的機制，讓memory可以被外部訊號可以更精細控制。如圖七所示，LSTM總共有3個Gate：1. input gate 2. forget gate 3. output gate，每個gate有被一個外部的訊號所控制，輸入訊號從下方進入神經元，首先經過input gate，input gate根據控制訊號，決定有多少量的輸入可以通過，Forget gate根據控制訊號，決定有多少原本存在記憶元的資料要保留，跟新的輸入混合，存入記憶單元。最後output gate根據控制訊號，決定要取出多少量的記憶單元資料輸出，跟一般神經元是一個輸入加一個輸出不同，LSTM是有四個輸入加一個輸出。 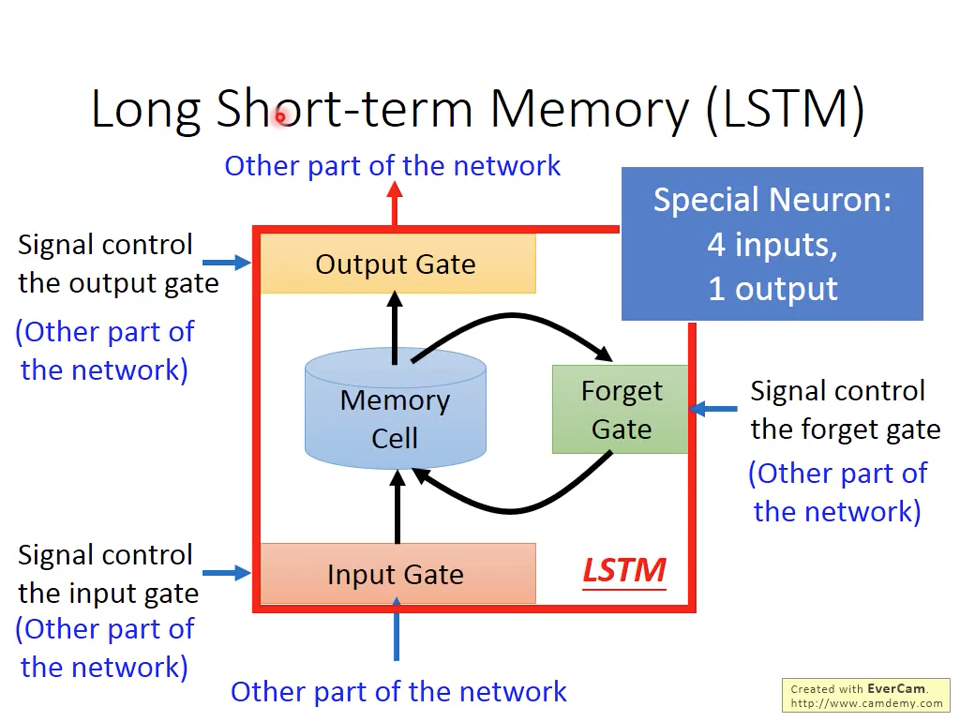圖七 Block View of LSTM

圖八更詳細解釋Gate數學模型，每個控制訊號$z_x$會經過一個activation function $f(\cdot)$再跟我們主訊號相乘，控制訊號的activation function通常會是sigmoid function，值域會在0~1之間，主要是模擬開關，開是0，關是1。我們在input gate跟output gate還各有一個activation function $g(\cdot)$, $h(\cdot)$來調整主訊號的值域，輸入訊號$z$通過input gate會產生$g(z)f(z_i)$的內部訊號，新的記憶$c'$會等於$g(z)f(z_i)$加上前一時刻記憶$c$乘上forget gate $f(z_f)$。輸出訊號$a$等於記憶$c'$通過一個activation function $h(\cdot)$ 乘以output gate $f(z_o)$。常見的$g(\cdot)$跟$h(\cdot)$會使用hyperbolic tangent $tanh$，主要模擬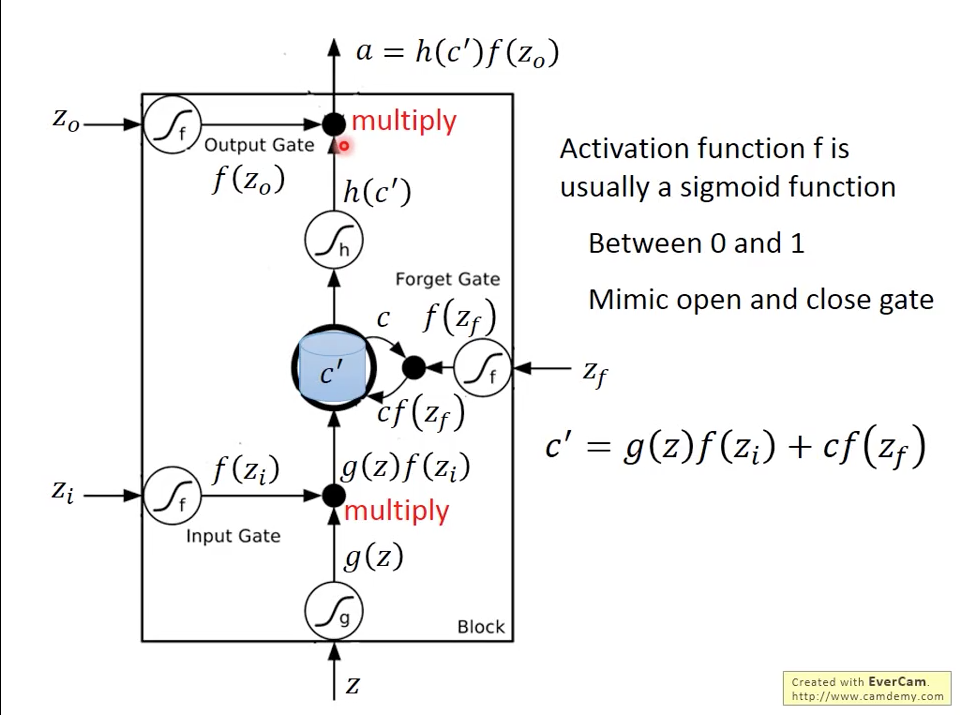資料壓縮$(-inf,inf) \to (-1,1)$。 圖八 Mathimatical View of LSTM

Illustrative Example of LSTM

舉一個簡單的例子，我們定義一組函數$y=f(x_1,x_2,x_3)$，這個函數有下列的規則：

1. $x_2=1$時，把$x_1$值寫入記憶$c$
2. $x_2=-1$時，把記憶$c$歸零
3. $x_3=1$時，把記憶$c$值輸出 如圖九所示，這個規則底下，我們有上半部黃色區域$x_1,x_2,x_3$的輸入序列，我們可以手解紅色區域$y$的輸出。 圖九 Example Sequence

LSTM可以用輸入訊號在每個gate乘上對應權重產生控制訊號，在這裡我們先不討論如何這些權重，假設我們已經得到這些權重。如圖十所示，$(x_1,x_2,x_3)$在輸入的權重是$(1,0,0)$加bias=0，input gate權重是$(0,100,0)$加bias=-10，forget gate權重是$(0,100,0)$加bias=10，output gate權重是$(0,0,100)$加bias=-10，為了簡化計算，我們假設$g(\cdot)$跟$h(\cdot)$都是linear function 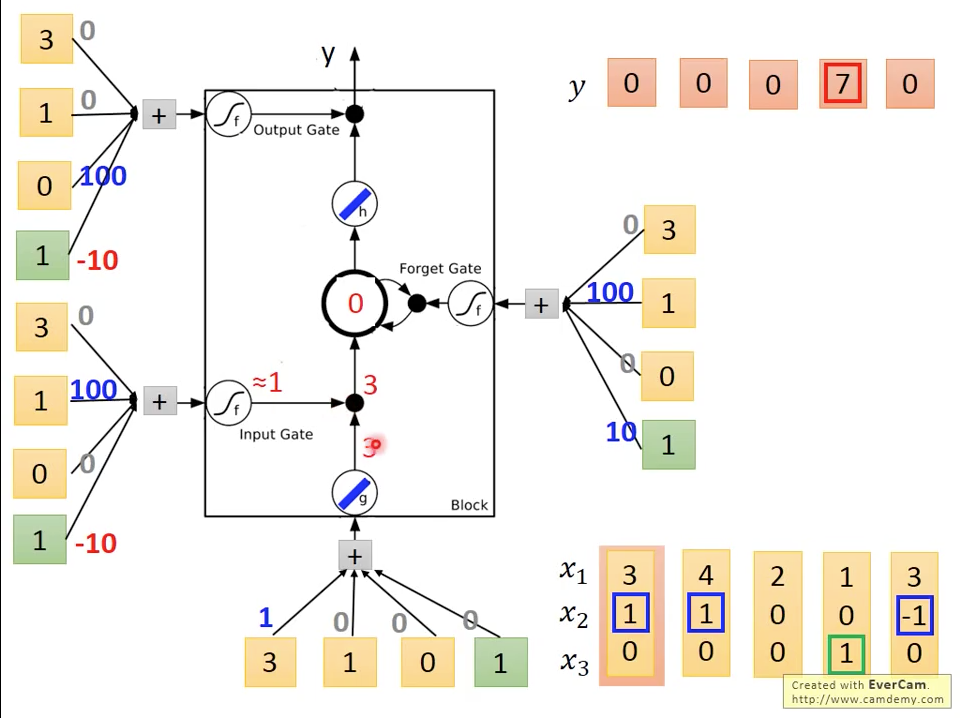$(y=x)$ 圖十 Time=1

第一個時間點，我們輸入端會得到$g(z)=3$，$f(z_i) \approx 1$，所以memory $c=0+f(z_i)g(z)=3$

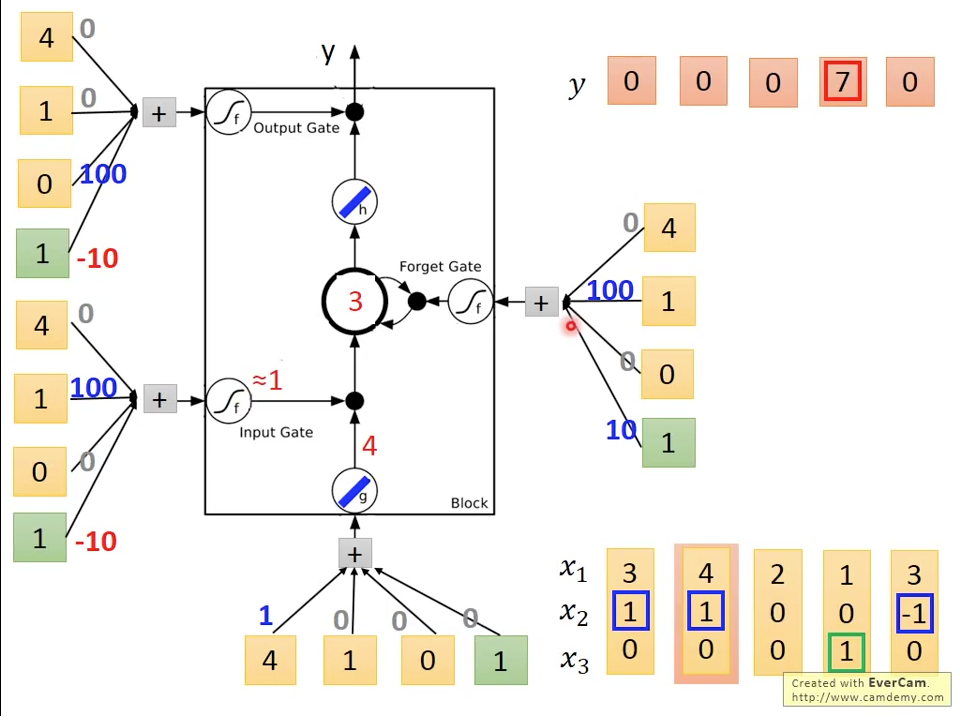圖十一 Time=2

第二個時間點，$x_1=2 \to g(z)=4$，$x_2=1 \to f(z_i) \approx 1$， $c'= c+f(z_i)g(z) = 3 + 1\times 4=7$

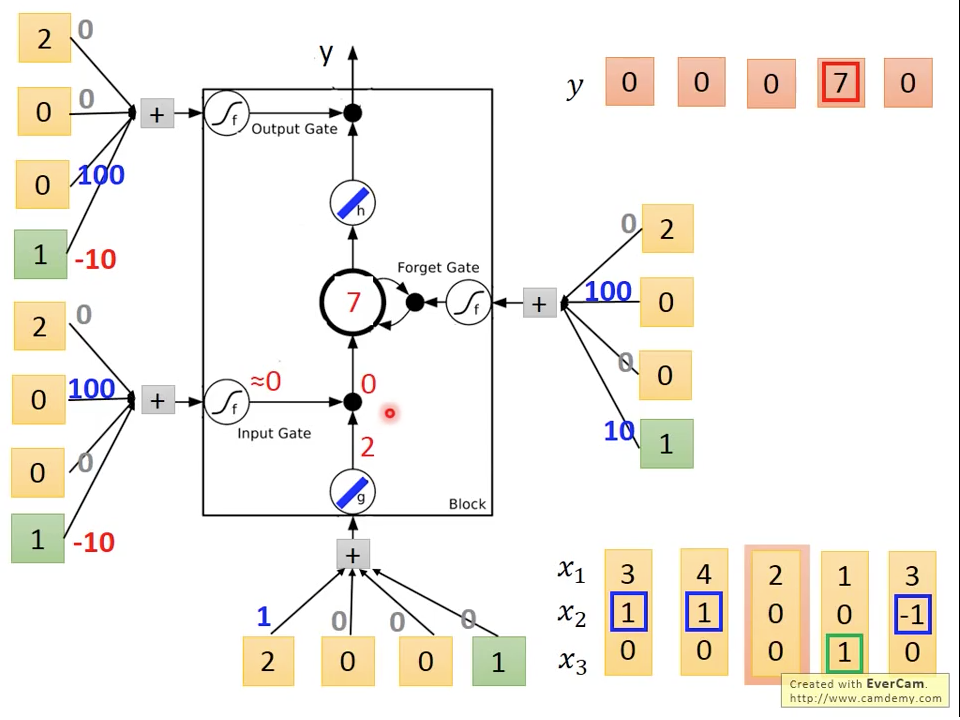圖十二 Time=3

第三個時間點，因為$x_2=0 \to f(z_i) \approx 0$，所以$f(z_i)g(z) = 0 \to c'= c = 7$

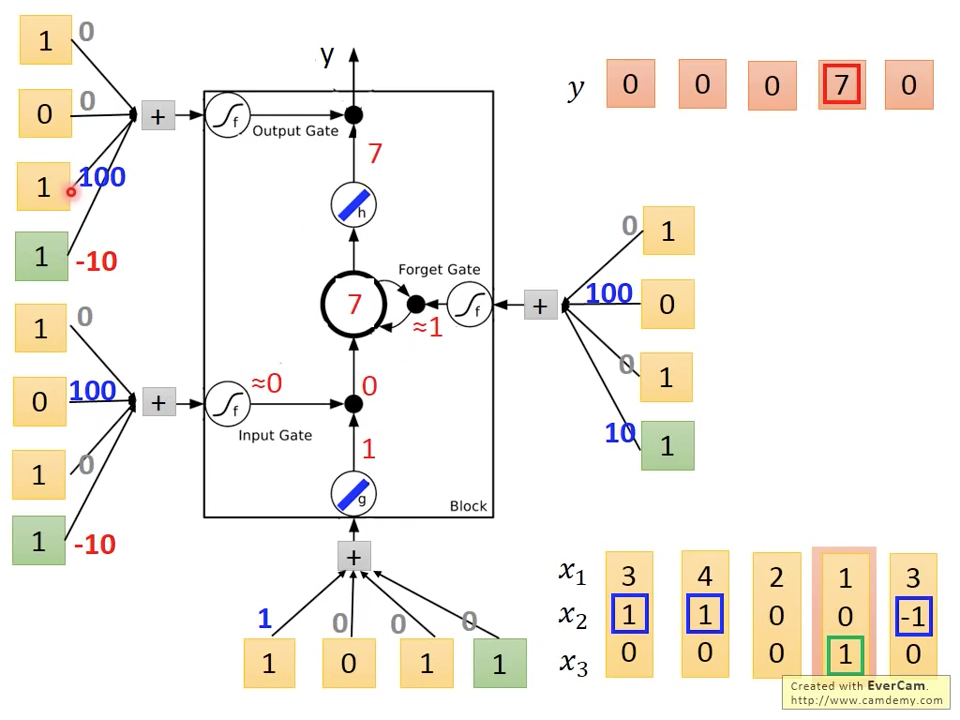圖十三 Time=4

第四個時間點因為$x_2=0 \to f(z_i)g(z) = 0 \times 1 = 0$，$c'=c=7$，但因為$x_3=1$，所以$f(z_o) \approx 1$，所以output $a= f(z_o)h(c')= 7$

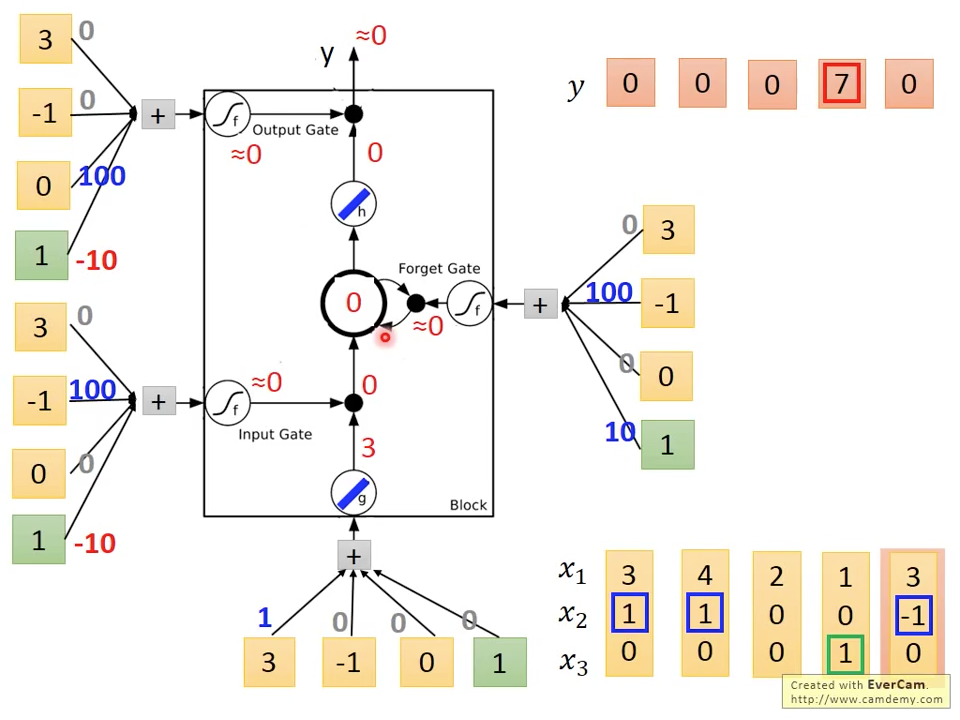圖十四 Time=5

第五個時間點因為$x_2=-1$，所以$f(z_i) \approx 0$, $f(z_f) \approx 0$，所以$c'= f(z_i)g(z) + cf(z_f)= 0 \times 3 + 7 \times 0 = 0$，output $a = f(z_o)h(c') = 0$。

simple RNN vs LSTM

當我們想把simple RNN換成LSTM時，如圖十五跟十六所示，只是把藍色的RNN神經元換成LSTM神經元就完成了，要稍微注意的是，因為跟simple rnn比起來，LSTM多了三個gate input，所以要訓練的參數也變成原本的四倍。 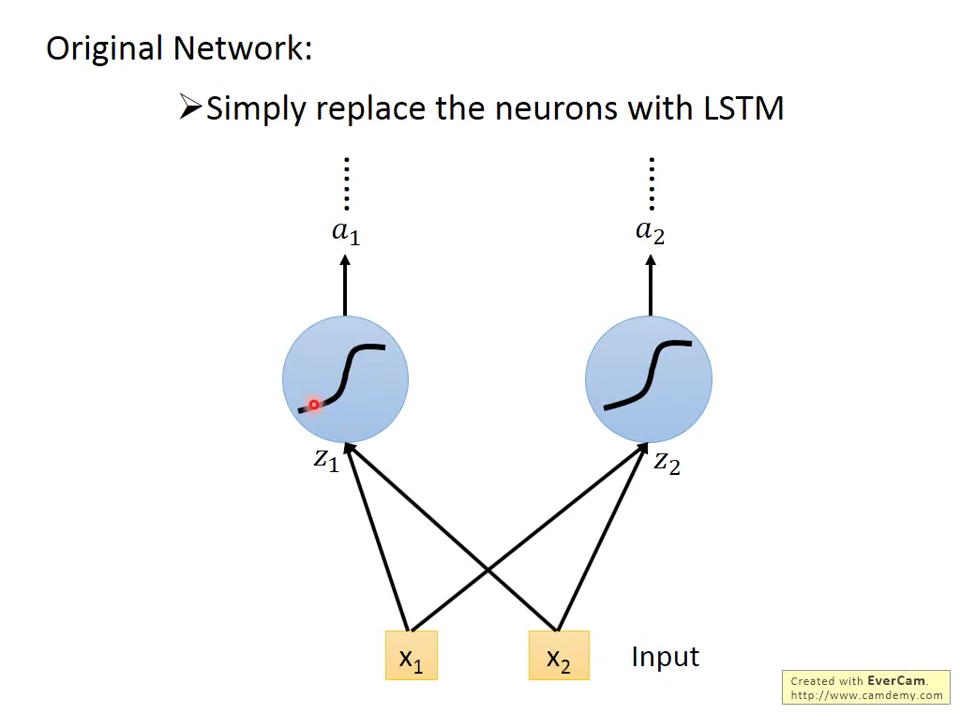圖十五 simple rnn

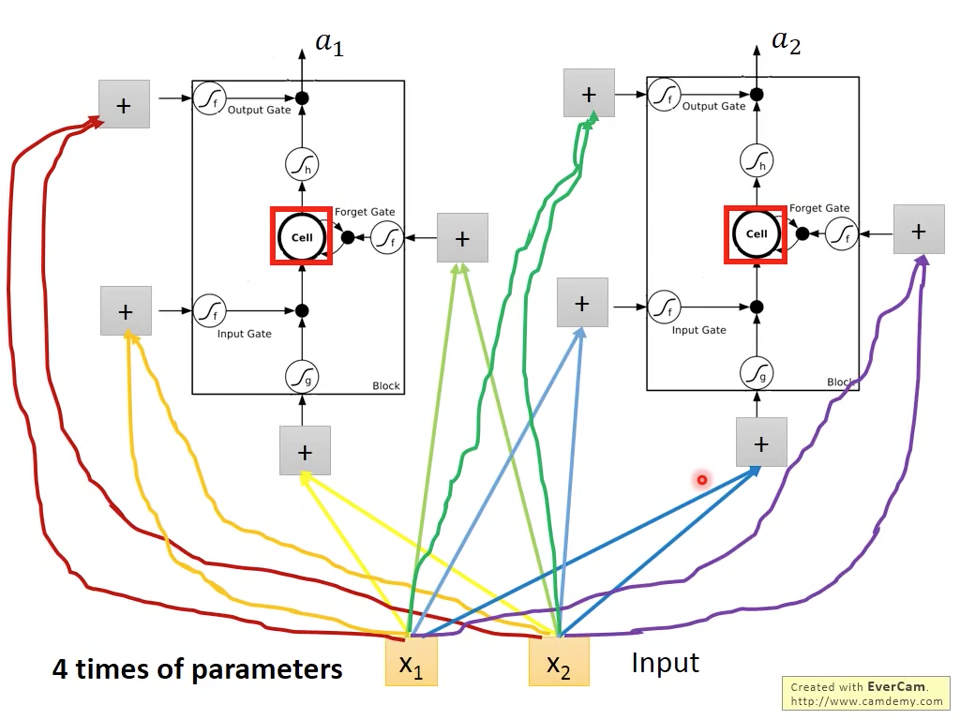圖十六 lstm neuron

Vector View of LSTM

在真實使用時，我們使用多個LSTM神經元並排在一起，形成一個記憶向量$\bar{c}^{t}$，在這種表示方式下，我們可以如圖十七～二十二那樣，重新描述LSTM的架構。圖十七表示，我們可以把輸入訊號向量$\bar{x}^t$乘上對應權重產生控制向量加主訊號$(\bar{z}_f,\bar{z}_i,\bar{z}_o,\bar{z})$，$z_x$的維度跟LSTM神經元數量相同。 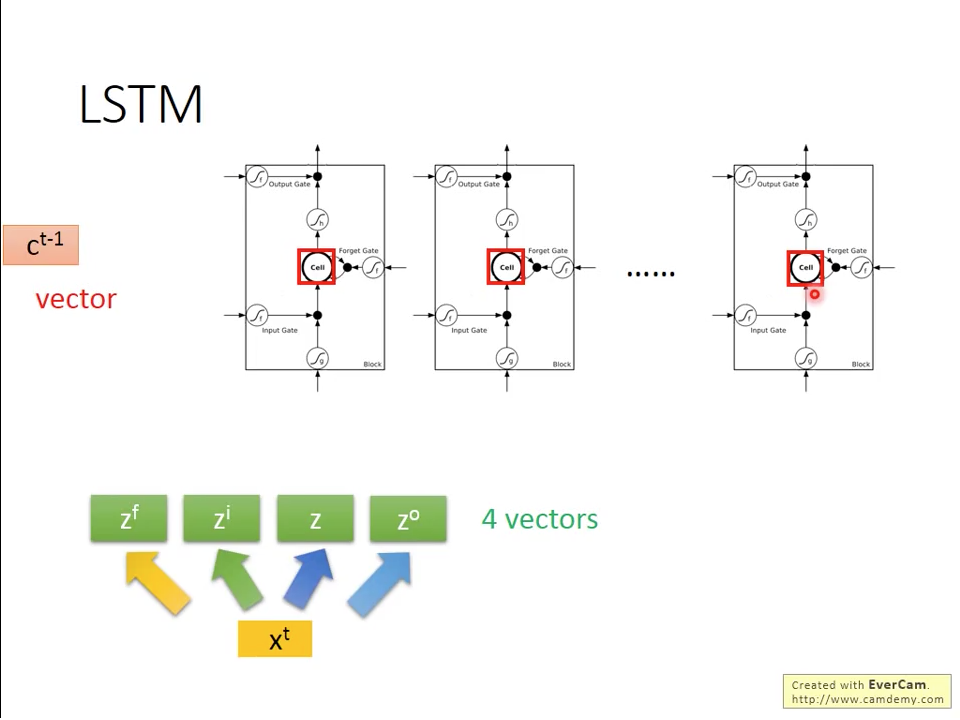圖十七 Vector

我們可以把LSTM的模型外型重新排列，從原本圖十八的右半邊，變成左半邊。

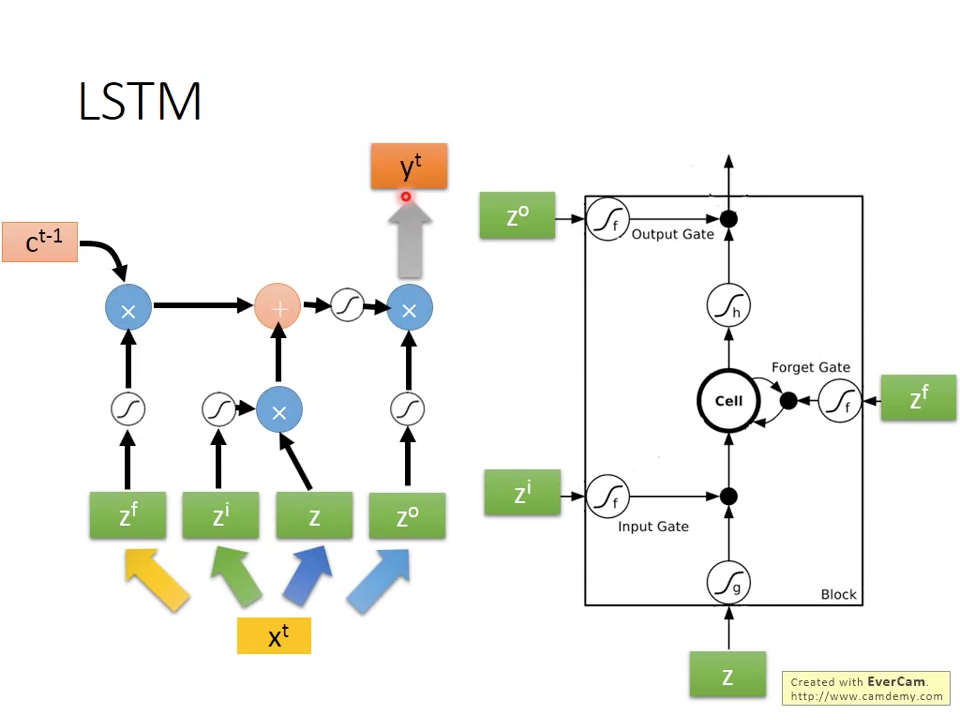圖十八 Reformulated LSTM

所以原本圖三seq2seq的模型，就會變成如圖十九所示，每個時間點都會從原本$\bar{c}^{t-1}$跟$\bar{x}^t$產生新的$\bar{c}^{t}$跟輸出$\bar{y}^t$，再往後傳遞

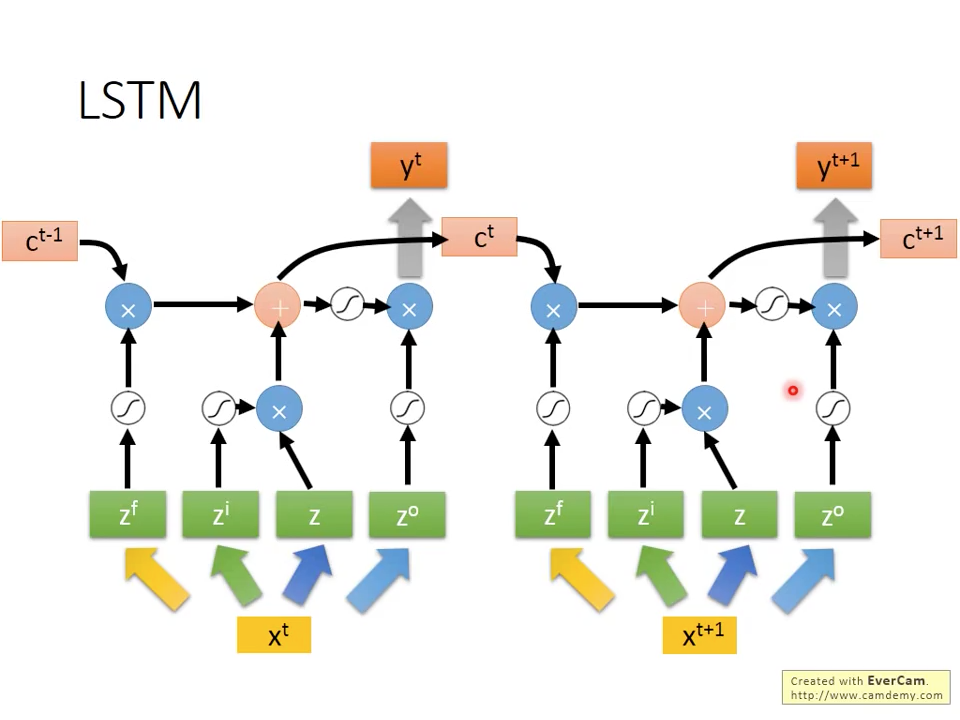圖十九 Seq2Seq LSTM without recurrent

真實的情況是，我們在產生$(\bar{z}_f,\bar{z}_i,\bar{z}_o,\bar{z})$，除了當下的訊號$\bar{x}^t$，還有前一個時間的output recurrent訊號$\bar{h}^{t-1}$，如圖二十所示。

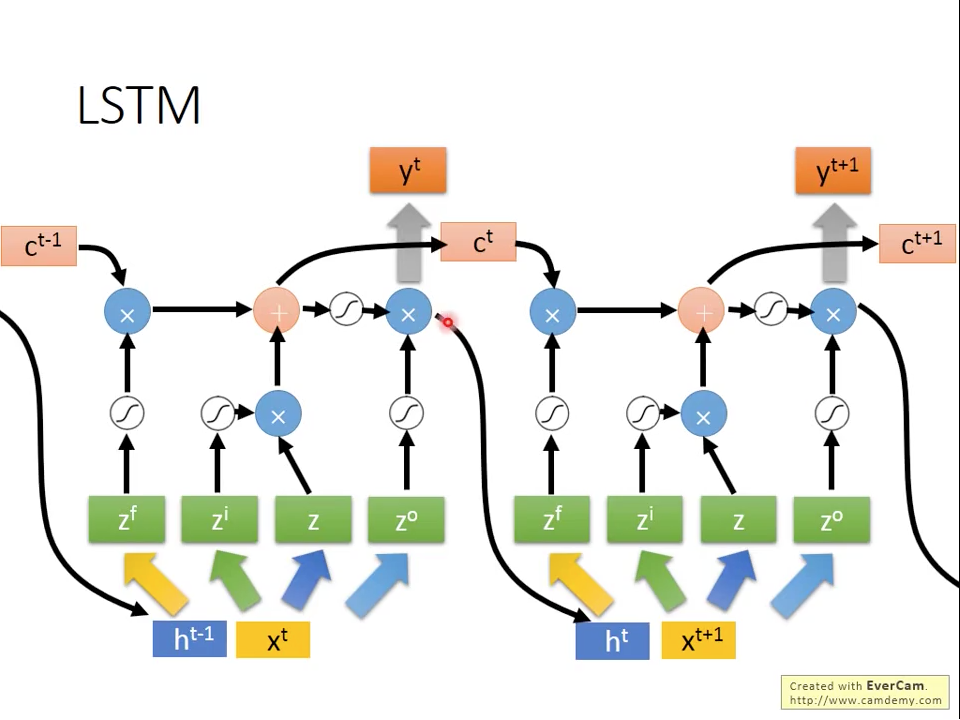圖二十 Seq2Seq LSTM with recurrent

更複雜的情況是，除了$\bar{x}^t$跟recurrent $\bar{h}^{t-1}$，還有前一個時間記憶$\bar{c}^{t-1}$也參與$(\bar{z}_f,\bar{z}_i,\bar{z}_o,\bar{z})$的產生，這種做法叫做peephole。

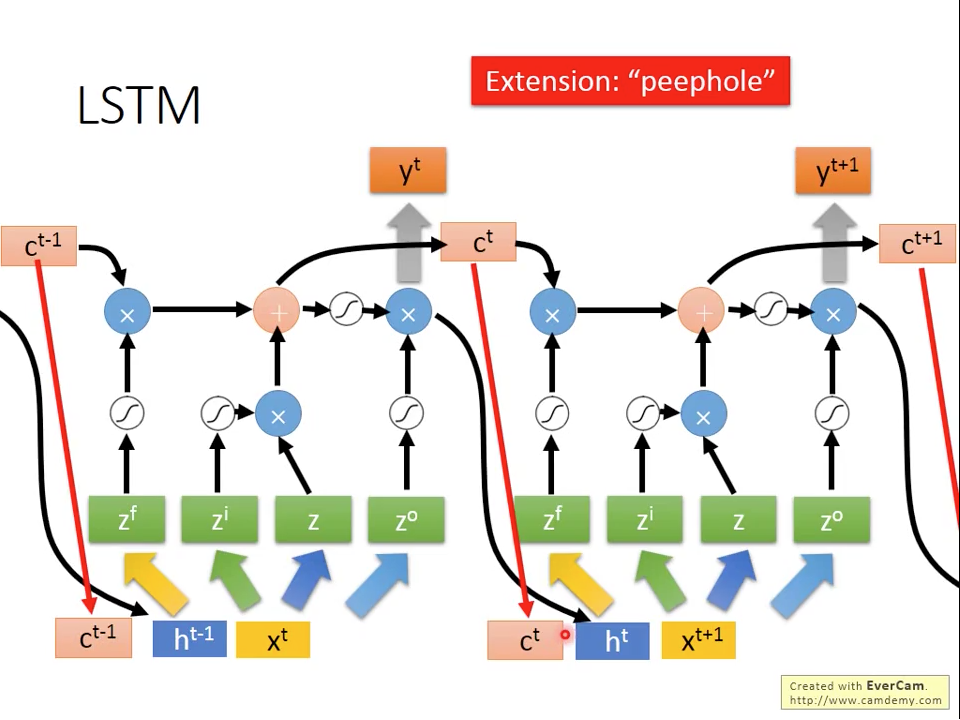圖二十一 peephole LSTM

LSTM的層數也不限於一層，如圖二十二所示，可以把多個單層的LSTM接在一起變成一個多層LSTM。 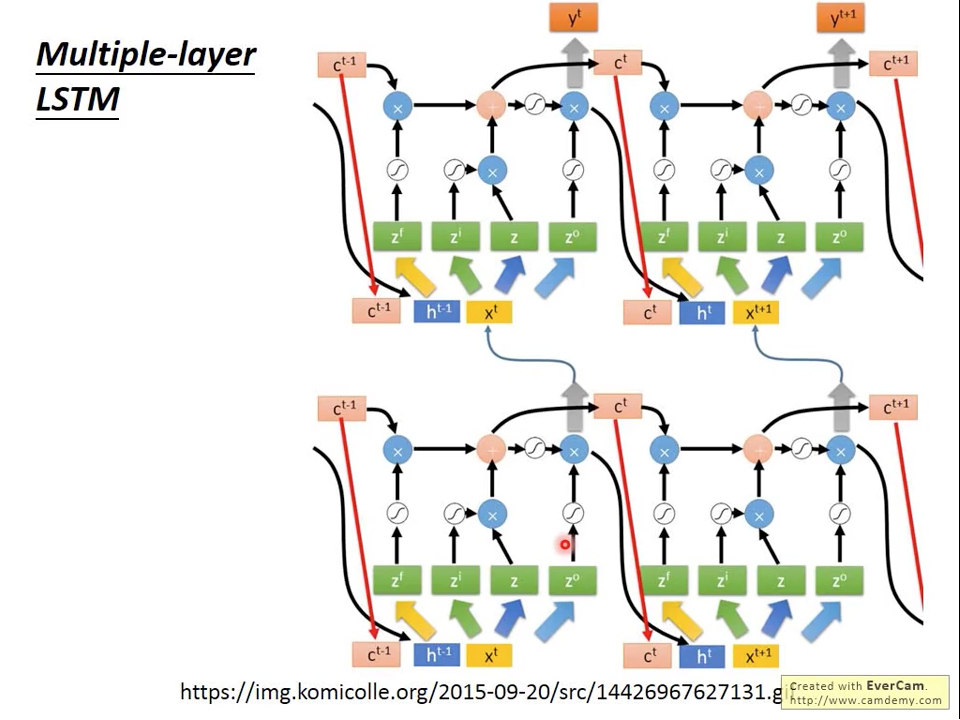圖二十二 Multi-Layer LSTM

雖然LSTM數學上運算比較複雜，不過現在主流的深度學習框架(eg:keras, tensorflow)都已經支援lstm的api，只需要簡單一兩行就可以呼叫內建的LSTM，在開發上可以省不少時間。另外要注意的是，現在研究人員提到他們有使用RNN模型時，絕大部分就是指LSTM或是另外一個參數比較少的Gated Recurrent Unit(GRU)，如果是最原始到RNN，則會用simple RNN來表示。

[0] ML Lecture 21-1: Recurrent Neural Network (Part I)